Find Missing Triangle Side: Easy Steps & Tips

<!DOCTYPE html>
Struggling to find the missing side of a triangle? Whether you’re solving a geometry problem or working on a real-world application, understanding how to calculate the missing side of a triangle is essential. This guide will walk you through easy steps and provide helpful tips to make the process seamless. From using the Pythagorean theorem to applying trigonometric ratios, you’ll master this skill in no time. (finding missing sides, triangle calculations, geometry tips)
Understanding the Basics of Triangle Sides

Before diving into calculations, it’s crucial to understand the types of triangles and their sides. Triangles can be classified based on their sides and angles: equilateral (all sides equal), isosceles (two sides equal), and scalene (all sides different). Knowing the type of triangle can simplify the process of finding the missing side. (triangle types, equilateral, isosceles, scalene)
Using the Pythagorean Theorem for Right Triangles
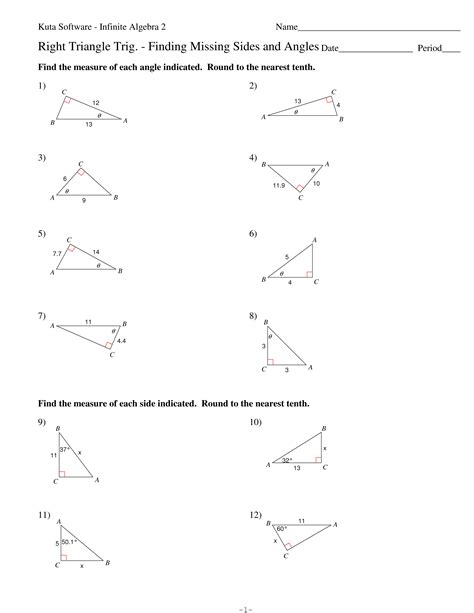
The Pythagorean theorem is a powerful tool for finding the missing side of a right triangle. It states: a² + b² = c², where c is the hypotenuse (the longest side). Follow these steps:
- Identify the known sides (a and b) and the unknown side ©.
- Plug the values into the formula.
- Solve for the missing side.
📌 Note: Ensure the triangle is a right triangle before applying this method.
Applying Trigonometric Ratios for Non-Right Triangles

For non-right triangles, trigonometric ratios (sine, cosine, tangent) are your go-to tools. Here’s how to use them:
- Identify the known angle and sides.
- Choose the appropriate ratio (e.g., sine for opposite/hypotenuse).
- Set up the equation and solve for the missing side.
| Ratio | Formula |
|---|---|
| Sine (sin) | sin(θ) = opposite / hypotenuse |
| Cosine (cos) | cos(θ) = adjacent / hypotenuse |
| Tangent (tan) | tan(θ) = opposite / adjacent |
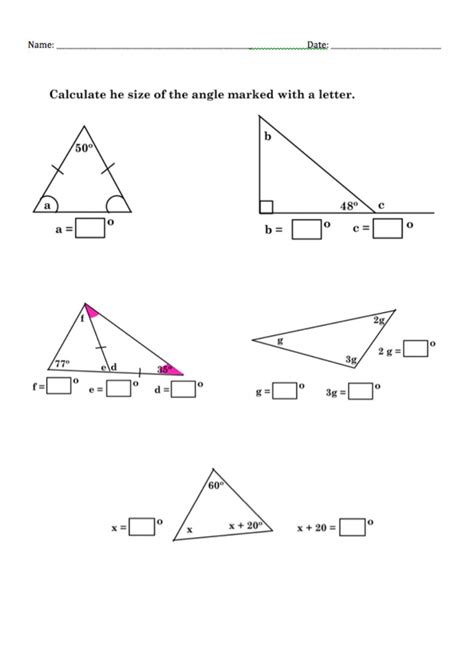
(trigonometric ratios, sine, cosine, tangent)
Using the Law of Cosines for Scalene Triangles
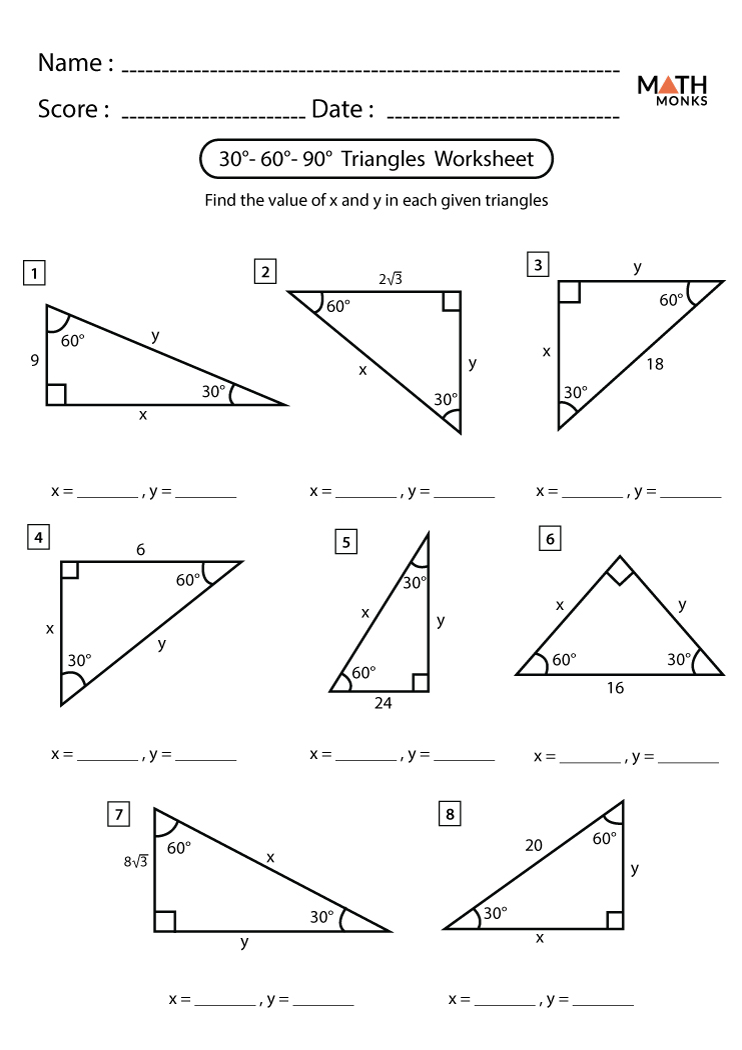
The Law of Cosines is ideal for finding the missing side of a scalene triangle. The formula is: *c² = a² + b² - 2abcos(θ). Here’s how to apply it:
- Identify the known sides (a and b) and the included angle (θ).
- Substitute the values into the formula.
- Solve for the missing side ©.
📌 Note: This method works for all triangle types, not just scalene.
Tips for Accurate Triangle Side Calculations
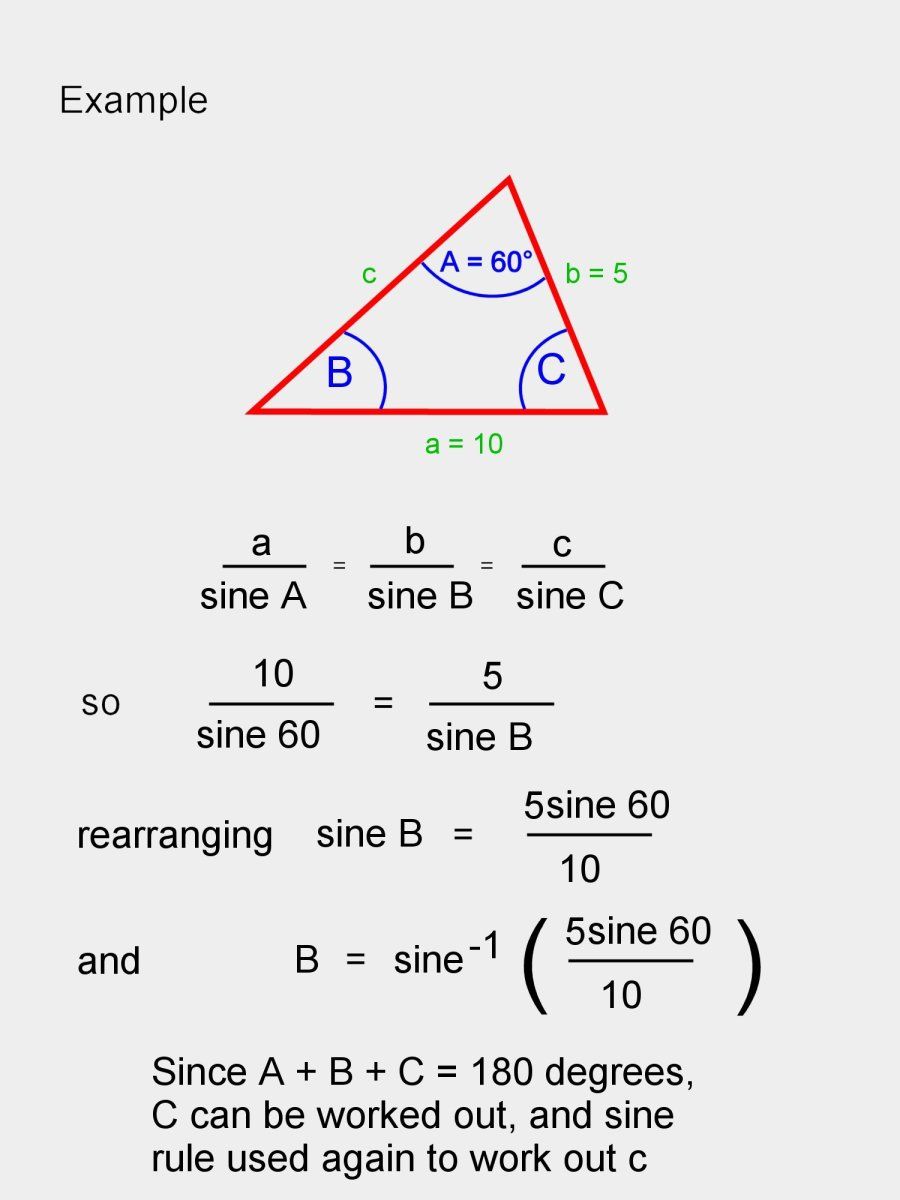
To ensure accuracy, keep these tips in mind:
- Double-check your measurements and angles.
- Use a calculator for precise trigonometric values.
- Label sides and angles clearly to avoid confusion.
(calculation tips, accuracy, measurements)
Finding the missing side of a triangle doesn’t have to be daunting. By understanding the triangle type and applying the right formula—whether the Pythagorean theorem, trigonometric ratios, or the Law of Cosines—you can solve any problem with confidence. Practice these steps, and you’ll become a pro in no time!
What is the Pythagorean theorem used for?
+The Pythagorean theorem is used to find the missing side of a right triangle, particularly the hypotenuse.
Can the Law of Cosines be used for right triangles?
+Yes, the Law of Cosines can be used for all triangle types, including right triangles, but the Pythagorean theorem is simpler for right triangles.
How do I choose the right trigonometric ratio?
+Choose the ratio based on the known and unknown sides: sine for opposite/hypotenuse, cosine for adjacent/hypotenuse, and tangent for opposite/adjacent.



