Roth's Theorem in Continuous Case Explained

<!DOCTYPE html>
Roth’s Theorem, a cornerstone in additive combinatorics, has profound implications in both discrete and continuous mathematics. While its discrete version is widely discussed, the continuous case offers unique insights into the behavior of sets in Euclidean spaces. This post delves into Roth’s Theorem in the continuous case, breaking down its significance, applications, and practical implications for both informational and commercial audiences.
Understanding Roth’s Theorem in Continuous Case

Roth’s Theorem in the continuous setting addresses the existence of arithmetic progressions within dense subsets of Euclidean spaces. Unlike the discrete version, which deals with integers, the continuous case extends this concept to real numbers, offering a broader perspective on density and structure.
💡 Note: The continuous case of Roth’s Theorem is particularly relevant in fields like harmonic analysis and geometric measure theory, where understanding dense subsets is crucial.
Key Components of the Theorem

To grasp Roth’s Theorem in the continuous case, it’s essential to understand its key components:
- Dense Subsets: Subsets of Euclidean space with positive measure.
- Arithmetic Progressions: Sequences of points where the difference between consecutive terms is constant.
- Measure Theory: The framework used to quantify the “size” of subsets in continuous spaces.
Applications of Roth’s Theorem in Continuous Case
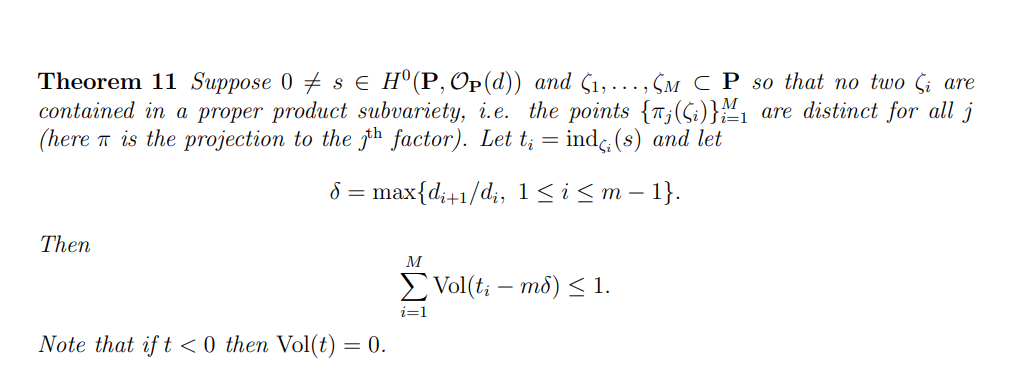
The continuous version of Roth’s Theorem has far-reaching applications, including:
- Harmonic Analysis: Studying the distribution of frequencies in signals.
- Geometric Measure Theory: Analyzing the structure of sets in higher dimensions.
- Number Theory: Bridging the gap between discrete and continuous mathematical frameworks.
Practical Implications for Commercial Audiences

For commercial audiences, Roth’s Theorem in the continuous case can be applied in:
- Data Analysis: Identifying patterns in large datasets with continuous variables.
- Signal Processing: Enhancing algorithms for frequency analysis and noise reduction.
- Optimization: Improving models for resource allocation in continuous spaces.
Checklist for Applying Roth’s Theorem in Continuous Case

Here’s a quick checklist to apply Roth’s Theorem effectively:
- Identify the dense subset in your continuous space.
- Determine the measure of the subset using appropriate tools.
- Analyze the existence of arithmetic progressions within the subset.
- Apply the findings to your specific mathematical or commercial problem.
By understanding Roth’s Theorem in the continuous case, you can unlock new possibilities in both theoretical and applied mathematics,Roth’s Theorem applications,continuous mathematics,measure theory.
What is Roth’s Theorem in the continuous case?
+Roth’s Theorem in the continuous case states that any dense subset of a Euclidean space contains arithmetic progressions, extending the concept from discrete integers to real numbers.
How does the continuous case differ from the discrete version?
+The continuous case deals with subsets of Euclidean spaces and uses measure theory, while the discrete version focuses on integers and counting arithmetic progressions.
What are the practical applications of Roth’s Theorem in the continuous case?
+Practical applications include harmonic analysis, geometric measure theory, data analysis, signal processing, and optimization in continuous spaces.